内部エネルギーとエンタルピーをわかりやすく解説！

今回のテーマは「内部エネルギー」です！

すっごいコアな内容ですね。でも「物理化学が分からない！」って人は、だいたいがここでつまづいているはずです。

すごく厳密な話をはじめから理解するよりも、定義を知って、それが使えるようになることがまずは重要です。

皆さんはスマホのしくみを知る前に、立派に使いこなしてスマホでゲームをやっていますよね？

勉強も同じです！まずはなんとなくイメージをして、使っていくうちに深く理解できることもあるのです。

分かるところまで頑張って取り組んでみて、実際に問題を解いて実践してみてください。

今回は、最終的にエンタルピーの定義まで繋げていきますので、ご興味のある方はご覧ください！

まずは「系」をイメージする！

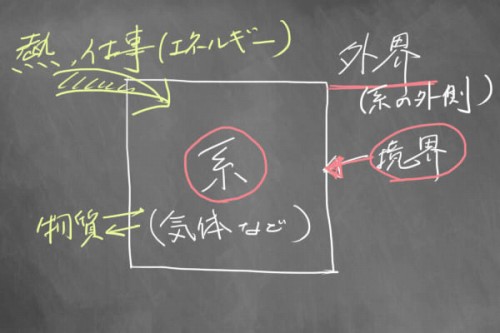
まず、物理学では、どんな状況でも「系（けい）」というものをイメージして、物事を考えないといけません。

簡単にいうと、系というのは「気体の入った箱」みたいなもので、その中で物質のなんらかの変化を観測していきます。

その箱以外のまわりの世界を「外界」とよび、箱そのものを「境界（系と外界を隔てるもの）」っていいます。

そして、「外部から熱を加える」とか「外部から仕事（力）を加える」というのは、文字通り「系の外側」からエネルギーを与えるということです。

で、ですね。「系」には大きく分けて４つあるので、ちゃんとイメージできるようにしておきましょう！

これが分からないと、物理化学はなんのこっちゃ？？になってしまうので、超基本になります。

開いた系（開放系）

境界を通して、物質およびエネルギー両方が移動できる

孤立系

文字通り、外界と何の交流もできない系。物質もエネルギーもどちらも移動できない。

閉鎖系

物質の交換はできないが、エネルギーは交換可能。

物質が出入りしないため、物質の質量は一定に保たれている。

断熱系

閉鎖系の一部とも考えられるが、エネルギーのうち熱の交換ができない系。

熱以外のエネルギー、例えば仕事などの交換は可能。

以上、この４つの系がありますので、それぞれの特徴はイメージできるようにしておきましょう！

内部エネルギーとは？

それでは、本題の内部エネルギーに入っていきましょう。

早速ですが、「系」という言葉を使っていきます。ここでは、閉鎖系をイメージしてもらえばいいかと思います。

それでは、ズバリ結論から。

内部エネルギーとは「その系の中にある全体のエネルギー」です。

具体的にどんなものがあるかというと、まずは分子の運動エネルギーです。気体をイメージしてもらえばよいのですが、１つ１つの分子は、常に動き回っていて、壁にぶつかっていますよね？

この分子の動きそのものが「熱」であり、壁にぶつかる力こそが「気体の圧力」になるわけです。

このような分子の運動エネルギーに加えて、構造エネルギーというものも含まれています。

これは何かっていうと、分子の中身のエネルギーのことです。原子同士の振動や、結合を介した回転運動、電子のエネルギーなど無数にあります。

こういったいろ～んなエネルギーをひっくるめて、内部エネルギーと定義して「U」と書いて表します。

そして、重要なことがひとつあります。物理学の世界では、内部エネルギーの絶対値を測ることはやりません！

大事なのは、反応前後での内部エネルギーの変化、つまり「ΔU」です（Δは「変化量」をあらわす）。

ΔUをみることで、熱や力などのエネルギーがどのように動いたのか？をみていくことになります。

熱と仕事で内部エネルギーは変化する！

では、実際に内部エネルギーを式で表していきます。といっても、めちゃくちゃ簡単な式なのでアレルギー反応は起こさないように！

内部エネルギーを変化させるものを考えると、「熱」を加えるか、「仕事（力）」を加えるか、しかないですよね？（ここではそういう仮定にしています！）

ここで、熱を「Q」、仕事を「W」とすると「ΔU＝Q+W」という式が書けます。与えられた熱と仕事が、内部エネルギーにプラスされるっていう式です。

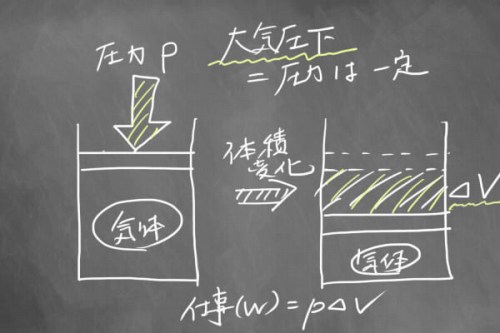
Wはもうちょっと別の書き方で表現できそうです。気体をイメージすると、仕事は体積を変化させてピストンを動かすようなイメージです。

もし大気圧下で圧力が一定だとすると、仕事量は圧力×体積変化で「pΔV」と表現することができます。

そして、もし気体が圧縮すればΔVはマイナス、膨張すればΔVはプラスになりますよね。

これを、気体の気持ちになって考えてみると、

気体が圧縮（ΔVは－）＝外部から仕事をされた＝内部エネルギーは増加（ΔUは+）

気体が膨張（ΔVは＋）＝外部に仕事をした＝内部エネルギーは減少（ΔUは－）

という関係になります。

つまり何が言いたいかというと、体積変化と仕事の符号が逆になるので仕事にはマイナスがつくのです！

ΔU＝Q－ｐΔVとなるわけですね。（ここが混乱するポイントかもしれません。この符号を間違えないように注意です）

これでΔUの定義は無事できました！

エンタルピーとは？

ここまできたら、エンタルピー（H）までもう一息です。

まずは、エンタルピーの定義というものを覚えましょう。これは、定義なのでこれ自体に意味はないので、気にしないように！

H＝U+pV

内部エネルギーと仕事（圧力×体積）の和をエンタルピーだと決めたわけです。

そして、内部エネルギーは「変化量」が大切だという話をしたように、この式においても変化量Δを考えていきます。

ΔH＝ΔU+Δ(pV)

もし、いま実験している系が「大気圧下」つまり「定圧変化」だとすると、pは一定になります。

ΔH＝ΔU+pΔV・・・①

ここで、もういちど内部エネルギーの式をみてみます。

ΔU＝Q－ｐΔV

⇒Q＝ΔU+pΔV・・・②

①と②をくらべてみると、ΔH＝Qとなりますよね！

ここが重要な結論になります。

定圧下（大気圧下でふつ～に実験すると）では、「系に出入りする「熱Q」はエンタルピー変化と同じになる」ということなのです。

これを絶対に忘れないようにしておきましょう！

まとめ

内部エネルギーは変化量が重要である。その変化量は、加えられた（放出した）熱と仕事で決まる。

ΔU=Q+W

定圧変化（大気圧下）ではW＝pΔVとなり、体積変化の符号を考えると

ΔU＝Q－pΔV・・・①とかける。

エンタルピーをHとして、H＝U+pV と定義する。

定圧変化では、その変化量は次のようになる。

ΔH＝ΔU+pΔV・・・②

①と②を比較すると、ΔH＝Qとなりエンタルピー変化は反応で出入りする熱量Qと同じになる。