今回は「エントロピー」についてまとめてみます。
理系の大学で勉強された人なら、きっと一度はぶち当たるであろう謎の概念ですね。
ちなみに。。。名前が似ているエンタルピーとはまったく異なる概念なので注意してくださいね!
エンタルピーについて復習したいという方はこちらの記事もどうぞ^^
それでは、早速エントロピーと仲良くなっていきましょう!
目次
エントロピーと乱雑さ!
いきなり質問ですが、皆さんは「お部屋の掃除」はお好きでしょうか?
好きな方のお部屋はきっと埃もなく、モノもきれいに整理されているはずです。
では、掃除があまり得意でない方のお部屋はどうでしょう?
脱ぎっぱなしの服があちらこちらに散乱し、漫画本も順序など関係なく乱雑に並べられているかもしれません。
では、この両者のお部屋の違いってなんなのでしょうか?
それは、「掃除」をしたか、しないか、の違いですよね。
どんなにきれいな部屋であっても、おそらく1か月も一切掃除をしなければ、「汚部屋」になってしまうことでしょう。
きれいに積まれた積み木があったとしても、風が吹いたり、誰かがちょっとぶつかっただけで簡単に崩れてしまいます。
人間もそう。教室のなかきれいに並んだ机で授業をじっと受けている生徒たちは、ベルが鳴った途端に席を立って、しまいには教室を飛び出していきます。
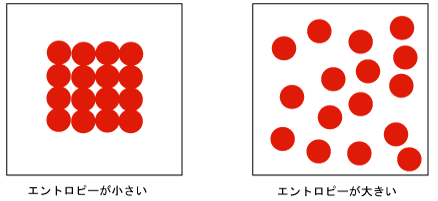
つまり、この世界にはどうも「放っておいたら乱雑になっていく」という性質がありそうです。乱雑さは増大するようにできているようです。
乱雑さの指標は何かないか?
言葉で「乱雑さ」といっても各々なんとなくイメージはできますが、その感覚は人それぞれです。
では、この乱雑さを測れる尺度を決めてしまおうということで登場したのが、「エントロピー」という数値(量)です。
では、実際に数式を使って表してみましょう。
たくさんのボールが一つの箱に入っていて、それぞれのボールが自由に動いている状況をイメージしてみてください。
あるボールの状態①(並び方)の出現確率をP1とし、それに対応するエントロピーをS1とします。一方、それとは異なる乱雑なボールの状態(並び方)の出現確率をP2、エントロピーをS2とします。
たとえば次のようなイメージしてみましょう。
①の状態 P1 S1
○○○○○○○○
②の状態 P2 S2
○ ○ ○
○ ○
○ ○ ○
エントロピーという新しい概念をせっかくつくるんだったら、扱いやすいように定義しちゃったほうがいいですよね。
エントロピー同士を足し算できると便利ですね。
①と②をまぜたときのエントロピーをS12としたときに、
S12=S1+S2とできると便利そうです。
そうなると、SとPをどのように結び付けて表わしたらいいだろうか・・・?
当時、哲学者であり、物理学者でもあったボルツマンは悩みました。
そしてあるとき、対数での表記を思いついたのです!
S=k・lnP(lnは自然対数・kは適当な係数)
対数の足し算はどうなったでしょう?対数同士の場合には、対数のなかは掛け算になりましたよね。
S12=S1+S2=k・lnP1 + k・lnP2 – k・ln(P1×P2)
つまり、確率(P)の掛け算になりますね!①と②を合わせたときの確率はP12=P1×P2ですから、この対数の定義はちょうどよさそうです。
こうして新たな概念エントロピーの原型が定義されました。
ゲームとエントロピー
では、実際にどんなところに使われているのかを、これからみていきましょう!
「ビット」という言葉を聞いたことはありますか?
テレビゲームをやったことのある方は、きっと一度は聞いたことがあるかもしれませんね。
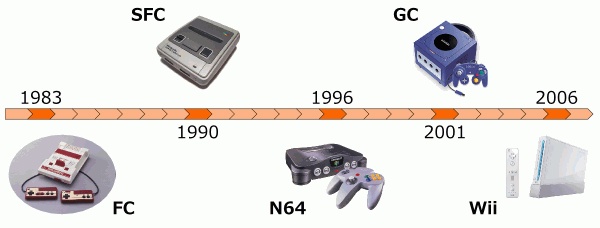
ファミコンは8ビット、スーパーファミコンは32ビット、ニンデントー64は64ビット、プレステ2は128ビット。
このビットというのは一体何か?
実はこれ、エントロピーに似た概念のひとつです。
「情報エントロピー(情報量)」という概念があります。
情報量(じょうほうりょう)やエントロピー(英: entropy)は、情報理論の概念で、あるできごと(事象)が起きた際、それがどれほど起こりにくいかを表す尺度である。ありふれたできごと(たとえば「風の音」)が起こったことを知ってもそれはたいした「情報」にはならないが、逆に珍しいできごと(たとえば「曲の演奏」)が起これば、それはより多くの「情報」を含んでいると考えられる。情報量はそのできごとが本質的にどの程度の情報を持つかの尺度であるとみなすこともできる。(wikipedia)
なんとなくイメージできますでしょうか?(笑)
事象 Eが起こる確率を P(E)とするとき、 事象 E が起こったことを知らされたとき受け取る(選択)情報量 I(E) を
I(E) =log(1/P(E))と定義します。
この対数の底を2にしたときに、情報量(bit)になります。
I = log2(1/P(E)) bit
なんで底を2にしたのか?
2つのものから1つを選ぶときの情報量を1bitと分かりやすく定義できるからです!
I=log{1/(1/2)}=log22=1
そして、2つの情報量の足し算は、上で説明したとおり掛け算にできます。
I1+I2=log(1/P1)+log(1/P2)=log{1/(P1×P2)}
例)サイコロを1回振ったとき「1の目が出た」という情報量は、
I=log26=log2(2×3)=log22+log23=1+1.58=2.58(bit)
となります。
では、「じゃんけん」ではどうなるでしょう?
AさんとBさんがジャンケンしたとき、「① Aが勝った」という情報と「② A がパーを出して負けた」という情報は、どちらが情報量が多いか?
どうでしょう・・・?
ジャンケンの組み合わせはグーチョキパーの3×3=9通りですよね。
①の場合の確率はグーチョキパーそれぞれで勝つ3通り。つまり、3/9=1/3。
②の場合の確率は当然ですが1通りです。つまり1/9。
情報量はそれぞれ、
①:I=log23=1.58
②:I=log29=log232=2×log23=3.16
ということは、②の情報量は①の2倍の情報量を含むということが分かるわけです!
おもしろくないですか?
情報量が多くなるということは、より具体的な描写ができるようになること、と言いかえてもらってもいいです。
①だと、3通りのうちのどれかであって具体的な勝ち方がはっきりしません。
一方、②だとAがパー、Bがチョキを出したという状況が1つに限定され、その状況はより具体的にはっきりイメージできますよね。
話を元にもどして、ゲームの画面を思い出してみください。
ゲーム機のビットというのは、CPU(ゲーム機の心臓)が一度に扱える情報量のことで、ビット数が高くなれば、より多くの情報を音や画面に出力できるということです。
ファミコンの画面って、処理能力なんだかブロックが粗くて細かい部分はぼやけていますよね。でも人の脳みそは優秀ですから、なんとなくそれが「人」だってわかるし、なんとなく「木」だってわかります。
一方、プレステ2とかになると、処理される情報量が膨大になっていますから、もはや実写のような詳細な情報を画面から得ることができるようになるのです。
いかがでしょうか?少しエントロピーが身近に感じてきましたか?
情報量とエントロピーの関係
ここで少し整理しておくと、エントロピーはそもそも「乱雑さ、あいまいさ」といったイメージをもつ概念でした。
一方で情報量は多くなると、より「具体的、鮮明になる」イメージです。
その計算式からも、確率の逆数の対数であらわされる量でした。つまり、確率が小さくなるほど(より起きにくい事象ほど)情報量が多くなるんですね。
なんとなく、エントロピーと情報の世界のつながりを感じてもらえればいいなと思います。
熱力学とエントロピー
ちょっと物理化学的なところにも触れていこうかと思います。
細かな数式の説明については、後ほどリンクを載せておくので、そちらで学んでもらえればと思います。
ここでは、おおまかなイメージを掴んでもらいたいので、そういう観点から説明します。
例えば、氷は放っておいたら溶けて水になります。
一度溶けてしまった氷は、そのままでは元には戻りません。
これを反応(現象)の「不可逆性」といいます。
ミクロでみていくと、氷の状態では水の分子がきれいに整列して配置して「乱雑さ」は低い状態にあります。
それが空気の熱を受けて、水の分子の運動が次第に大きくなり、配列がバラバラになって動き回れるようになり、乱雑さが増した状態になります。
氷が解けて水になるって感覚的には当たり前のことですが、「なんでもとに戻らないの?」っていうのを、数値化して目に見える形で表現できるって画期的なことなわけです。
こういう明らかな反応から、さまざまな条件での微妙な反応まで、数値化してその反応の不可逆性を知り、言い換えれば未来予測ができるようになるのです。
そして、エントロピー増大という宇宙の法則があります。
基本的には、エントロピーが大きくなる反応は自然に起こって元には戻らないと考えてよいわけですが、それは宇宙全体(閉じた系ともいう)としてみたとき、の話です。
実際の実験室で行われる反応では、熱してみたり、冷やしてみたり、圧力をかけたり、さまざまな条件を変えて行われるために、単純にエントロピーが大きくなる反応だけではないわけですね。
なので、残念ながらエントロピーの概念だけでは不十分で、エンタルピーとか、ギブスの自由エネルギーという概念が登場してきます。
こうやってわけが分からなくなる人が続出するんですね(汗
全部説明していくと、さすがに終わりそうもないので、今回はエントロピーに関してちょっとでも関心をもってもらえたら御の字ということで(笑
ネットには、わかりやすい説明たくさん転がっていますので、ぜひそれと合わせてイメージをつけていってもらえればと思います。
最後までお読みいただきありがとうございました!
<参考になるリンク>
コメント
物理化学で、めちゃんこ理解に苦しんでいた猫好きですが、今回の記事を読み、気が付きました。そう、エントロピーが、乱雑さかげんを示しているのと、そのうえで、大まかな
現象をなんとか理解できそうです。今回の記事を見て、しっかり勉強につなげられるように頑張ります。