薬物動態学×半減期
－dX/dt＝ke・X
－dX/dt：薬物消失速度
X：体内薬物量
ke：消失速度定数
この式がぴんと来ていない場合は、
第1回～第4回をみてください＾＾
では、半減期を計算するために、
この式を変形しましょう。
1/X・dX＝－ke・dt
これをt：0 ⇒t、X：Xo⇒Xで積分すると、
lnX=－ke・t＋lnXo
となります。
（ここは数学なので、忘れた時は復習を！）
Xは体内薬物量で、C（血中濃度）はXに比例するので、
lnC＝－ke・t＋lnCo
と表せます。
では、半減期のイメージ図です。
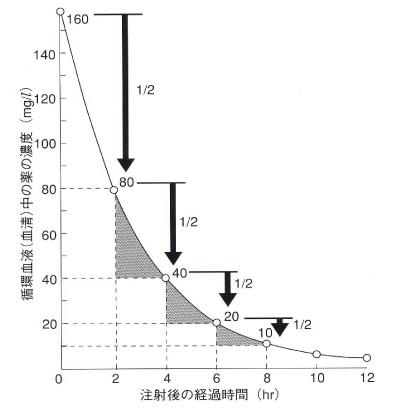
引用元：日本臨床薬理学会
これをみると分かりますが、
スタートの血中濃度に関わらず、
半減期（濃度が半分まで減る時間）は一定です。
これは、「薬物量に応じて消失（代謝）速度が変化する」
ことから起こる現象なのです。
ではさっきの式に、
t=t1/2、C＝1/2Coを代入すると、
ln（1/2Co）＝－ke・t1/2＋lnCo
t1/2＝ln2 / ke
⇒t 1/2＝0.693 / ke
これも覚えて使っていく式になってきますが、
忘れても簡単に導くことができます。
半減期は放射性物質などでも観測される現象ですが、
薬物動態学では最も肝となる指標となります。
その原理・しくみをしっかりと理解しておくことが大切です。