【統計学】相対リスクと95%信頼区間とは？

最近、とある後輩から
おもしろい活動をしている人たちがいる
という情報をGETしました。

 

その名もJJCLIP（じぇじぇくりっぷ）
あの朝ドラの流行語をもじって
ネーミングをしているそうです（笑

 

どんな活動かというと、
論文をよんで、実際の症例について
みんなで考えてみよう！というものだそうです。

 

英語論文なので、
ややハードルは高めかもしれないですが、
解説している方々がすごく分かりやすく
説明してくれているので、楽しく参加できると思います。

 

一応ご興味のある方のために
HPリンクを貼っておきます。
⇒JJCLIP

 

はい！では今回のテーマに移ります。
とっつきづらい統計学からピックアップです。
論文を読むには必要になる知識なのでまとめておきます。

 

間違っているぞ！というときは
ご指摘いただけるとありがたいです＾＾；
では、はじめます！

 

◆「相対リスク」って何のこと？ 

まず、薬の効果について評価するとき
にでてくる「相対リスク」について
復習していきます。

 

薬物治療でも外科治療でも、
”なぜ”行うのか？というと、
それは当然、病気を治すためであったり
生存率やＱＯＬをあげるためですよね。

 

もしもベネフィット（利益）がなければ、
コストや副作用などのリスクがあるため、
治療は行わないほうがよいということになります。

 

莫大な治療費をかけ、
患者さんを危険にさらしてまで、
効果が証明されていない治療はしたくないですよね？

 

では、どうしたら
ある治療が意味のあるものだ、
ということを証明できるのでしょうか？

 

現在用いられているのが、
統計学による評価・証明です。

 

具体的な試験方法としては、
二重盲検ランダム化比較試験
という臨床試験が行われています。

 

試験をするには、
実薬（評価したい薬剤）と
プラセボ（もしくは比較したい薬剤）
を用意する必要があります。

 

そして、どちらを飲むのか、
それらをランダムに被験者たちに
割り付けて試験を開始します。
これをランダム化というわけです。

 

二重盲検とは、
医療スタッフ（医師やその他の医療関係者）
被験者（治療をうける患者）両者とも
割り付けについて知らされない状態で試験を行うということです。

 

つまり、試験に直接関わる人たちは
プラセボか実薬かをまったく知らずに
臨床試験を進めていくことになります。

 

こういう手続きをして、
はじめて純粋な薬の効果
を評価できると考えられているのです。

 

人為的な偏りやプラセボ効果の
影響を最小限に抑える必要があるのです。
そうして得られたデータを第三者が統計処理を行っていきます。

 

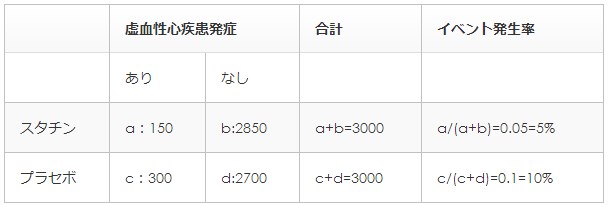
それでは実際にスタチンの
心血管イベントの抑制効果について
得られたデータで確認していきましょう。

 

 

数字はあえてシンプルにしています。
ただ、基本の考え方は実際の臨床試験でも変わりません。

 

相対リスクは、
（実薬でのイベント発生率）／（プラセボのイベント発生率）です。
イベント＝心筋梗塞や脳梗塞などの心血管イベントです。

 

表のデータから計算すると、
0.05／0.1＝0.5＝50%
となります。

 

つまり、スタチンを投与すると、
何も治療しない場合と比較して、
虚血性心疾患を起こす人の割合を
100%－50%＝50%下げるということになります。

 

これが相対リスクという考え方です。
なるほど！50%もリスクを下げるのか！
これはすごい！と感じるかもしれません。
（※実際この値はかなり高い数値です）

 

しかしここで、
注意しなければならないことがあります。
もともとのイベント発生率がどの程度だったか？という視点です。

 

今回はプラセボでの
イベント発生率が10%と高めに設定しましたが
もし0.1%だったらどうでしょう？

 

そもそもの発生人数は3000人のうち3人になります。
この人たち全員にスタチンを投与したときに救える人は
1人か2人ということになります。

 

こういう場合はすごく難しくなります。
薬である以上は当然ですが、
一定の割合で副作用が発生します。

 

リスクとベネフィットを考えたとき、
もしかするとスタチンによる治療は
行わない方がよいと判断されるかもしれません。

 

ですから、統計の数値をみるときには
背景の情報と他の因子についても
しっかりと考慮していく必要があるのです。

 

◆信頼区間って何のこと？

では次に「信頼区間」について
説明していきます。

 

よく用いられる表記としては、例えば、
相対リスク：0.8
95%信頼区間（0.62－0.95）
といった表記です。

 

この「信頼区間」って何のこと？
と疑問について解説していきます。

 

まず大前提として
統計学の目的は何かというと
「宇宙の真実」に近づくということです。
（話がでかい！）

 

たとえば、上のスタチンの例では、
全人類に協力してもらったときに
真実に最も近いデｰタが得られるわけです。
（※人種差とかはここでは無視）

 

ここでいう全人類というのが
「母集団」というものです。

 

そして、母集団すべてデータから
求めた「相対リスク」が真の値なわけです。
本当であれば、すべての臨床試験は
人類全体で行いたいわけです。

 

でも、そんなこと不可能ですよね(笑？
僕たちにできることは、全人類から
せいぜい数百、数千の人（サンプル）を抽出して試験を行うことです。

 

「真実はいつも一つ！」って
どこかの探偵が言っていた気がしますが、
真実の値はただひとつ世界に存在するのです。

 

その真の値と、
今回集めた数百人のデータから求めた値を
比較したときに、どの程度信頼できるの？
という目安が欲しいわけです。

 

そこででてくるのが
「95%信頼区間」という考え方です。

 

95%信頼区間（0.62－0.95）
という表記をみたときに
どのようにとらえるでしょうか？

 

「真の相対リスク値」が95%の確率で、
この0.62－0.95の区間内にある、
ということではありません！

 

これがよく間違いやすい
勘違いらしいです・・・
（ややこしい！）

 

ここでいう95%は・・・！？

今回得られたデータ（例えば100人分）
を使用して統計処理をしたとき、
その統計処理自体の信頼性を表わすものです。

 

真の相対リスクは、
そもそも変動するものではなく、
はじめから決まっているものです。

 

その真の値をどれほどの信頼性を
もって推定できますか？というのが
統計学に課された使命なわけです。

 

で、95%信頼区間（0.62－0.95）
が表す意味はというと、

 

100回同じように100人のサンプルを
集めて統計処理して、信頼区間を設定したとき、
95回はその区間内に「真の相対リスク」を
とらえることができるだろう、ということです。

 

あくまで、「95%」という数字は
統計処理自体の正確性を示している
と考えるべきなのです。

 

例えば99%に信頼度を設定すると、
信頼区間をもっと広めないといけなくなります。

 

区間が広い方が、
より真の相対リスクを捉える確率が
上がるからですね。

 

まぁ、もっと簡単に、
「実際に治療すると95%くらいは
この区間の中には入ってくるのね～」
くらいに考えてもいいかもしれません（笑

 

う～んややこしい！
もっとうまく説明できるといいですが・・・
補足説明などあればお願いします！