今回はよくでてくる用語解説として、
「コンパートメントモデル」について説明していきたいと思います。
早速ですが、
コンパートメントって何かというと、「箱」のことです。
ヒトの体はすごく複雑なので、一見すると薬の動きなど予想できないかに見えます。
それをどうにかしてシンプルにできないか?と考えたわけです。
そこで生まれたのがコンパートメントモデル=箱なのです。
薬は血中に入って全身を巡り。。。
肝臓で代謝され、腎臓で代謝され。。。
などはこのモデルにおいては一切関係ないのです。
つまり、
そういうミクロなところをみるのではなく、
体全体(マクロ)としてみたとき薬の動きについてみているのです。
本来は複雑な体内を、水が詰まった単純な箱と捉えて考えてきましょう!ということです。
分布容積の解説でも例えたように「フラスコ」と考えてもいいです。
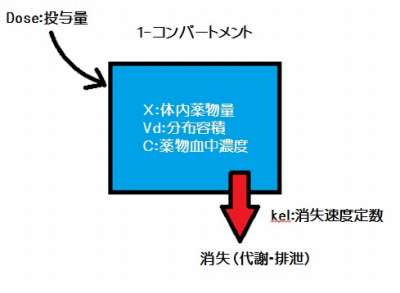
真ん中の箱が”ヒトの体内”です。
薬がこの箱の中に入って(投与)、出ていく(排泄)されるという単純なイメージです。
分布容積はこの箱の大きさ(=水の量)というわけです。
こうやってすごーくシンプルに体内をイメージすることで
簡単に計算ができて薬の動きを説明できるようになります。
では、ちょっと計算について説明します。
まず、静脈内注射であれば、
そのまま全量が身体の中に入るので、
Dose(投与量)=X(体内薬物量)になります。
X(薬物量 g) ÷ Vd(容積 L)=C(薬物濃度 g/L)はすぐにイメージできます。
これを変形すると、
Vd=X / Cとなるので「分布容積」が計算できるんです。
Vdっていうのは、箱(フラスコ)の容積であり、
これが大きいということは、
薬物が血中以外の組織に広がっていることを意味するわけです。
(血中にだけ存在すればVd=血液量となるので!)
実際にどう測定するか?についてです。
ある薬物(線形薬物で1-コンパートメント)を静脈内注射すると、時間と血中濃度のグラフは次のようになります。
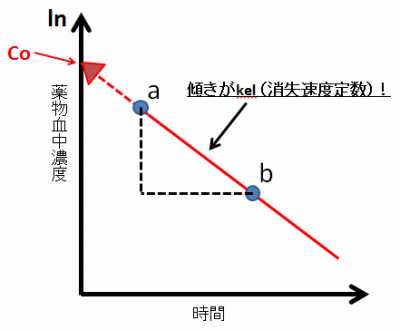
薬を投与したあと、a点とb点の2回血中濃度を測定します。
1次速度で薬が消失すると想定すると、グラフは直線になるので、a点とb点を結ぶ直線を引くことができます。
この時、縦軸にぶつかったところがCo(投与直後の血中濃度)になります。
ということは、
Xo/Co=Vdという計算ができるので、
投与した薬の分布容積が計算できるというわけです。
なおかつこのグラフからは、
kel(消失速度定数)も計算できるので
一度に二度おいしいグラフになっているのです。
すると、クリアランスや半減期・・・etc
薬物動態学でおなじみのパラメータも導くことができます。
多数の患者のデータを集めて、パソコンに取り込めばソフトがつくれます。
そうして患者データ(体重・年齢・性別・肝・腎機能)を入力すれば、ある程度の血中濃度推移が予測できるようになるのです。
「ヒトの体内を1つの箱に例えてみる」という発想がスタートになって、このような計算ができるようになったのです。
こうしてみるとすごく単純ですが、これって結構すごいことだと思います。
物事は複雑にすることは簡単ですが、シンプルにするのは難しいことが多いと思います。
「コンパートメント」という考え方はしっかりおさえておきましょう。
以上、図なども使って説明してみました。
最後までありがとうございました!